ど~も
お餅ROIです
義務教育のとき周囲を見ていて感じていたことは、数学を苦手と感じている人が多いなぁと思っていました。
数学が得意な理系のクラスへ行っても、この三角関数を苦手にする人が多いなぁと感じていました。
なので、三角関数について専門用語をなるべく使わずにサクッと使いこなせる方法を伝授します。
では、いきましょう。
三角関数とは

三角関数とは、sin、cos、tanがでてくるやつですね。
これがsin30度の時は、1/2になるよ。とか言うあれです。
以下に簡略表を添付します。
| sinΘ | cosΘ | tanΘ | |
| 0度 | 0 | 1 | 0 |
| 30度 | √1/2 | √3/2 | 1/√3 |
| 45度 | √2/2 | √2/2 | 1 |
| 60度 | √3/2 | √1/2 | √3 |
| 90度 | 1 | 0 | ∞ |
こんなのです。思い出しましたか?
三角関数を苦手にする理由
苦手にする理由は、とにかく覚えることが多いことです。
そして、覚えただけでは試験問題が解けないことです。
つまり、ちゃんと理解して使いこなさなきゃいけない所なのです。
これらの2点の原因でほとんどの人が挫折しています。
三角関数で覚えること

基本的には三角関数で覚えることは以下の4つです。
- ピタゴラスの定理
- 公式2つ
- All STC(オールスティック)
- sinΘの変換値
- 直角三角形になる比率(覚えなくてもいい)
ピタゴラスの定理
以下の図で示した様に、ヨコとタテの2乗がナナメの2乗になりますよ。と言う公式です。
そして、これが成り立つときは必ず直角三角形になりますよ。と言う公式です。
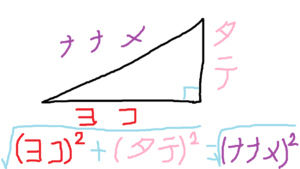
また、cosΘ=ヨコ÷ナナメ、sinΘ=タテ÷ナナメ、tanΘ=タテ÷ヨコです。
補足知識
ここは、補足知識なので読まなくてもいいです。
ピタゴラスの定理のヨコとタテを3以上乗にして、ナナメの3以上乗(ヨコとタテと同じ乗数)は存在しないと言うことを証明しなさい。と言うのがフェルマーの最終定理です。
数百年以上前に生きていた裁判官の偉人が家にいるときに暇すぎて作った問題だそうです。
そして300年くらい誰一人証明できなかったそうです・・・w
まず間違いなくフェルマーの最終定理は試験で出ないです。
そして、日常生活で使うことはないので、覚える必要性は全くないです。
東京大学の2次試験にでるかも?くらいの問題です。
覚えるメリットは、周りの人に知っている自慢が出来るだけでしょうね。
つまり、不要です。
公式2つ
覚える公式は色々ありますが、とりあえず以下の2つだけでいいです。
sinΘの2乗 + cosΘの2乗 = 1 (これは、Sの2乗+Cの2乗=1と簡略化)
sinΘ ÷ cosΘ = tanΘ (これは、S÷C=Tと簡略化)
All STC(オールスティック)
以下の図も三角関数で、よく見るものだと思います。
All STC(オールスティック)の意味を説明します。
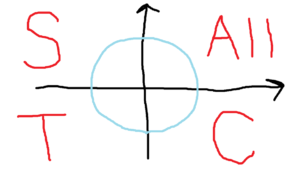
Θが0~90度の時はsin、cos、tan全てがプラスです。
Θが90~180度の時はsinのみがプラスです。(他はマイナス)
Θが180~270度の時はtanのみがプラスです。(他はマイナス)
Θが270~360度の時はcosのみがプラスです。(他はマイナス)
つまり、どこがプラスなのか暗記するの呪文がAll STC(オールスティック)です。
sinΘの変換数値
以下で全ての変換数値を表にしました。
示したように、たくさんの数値を覚えないといけないように感じる人も多いと思います。
しかし実は覚えるのは、赤数値のsinΘの0~90度までの5つのみでいいです。
| sinΘ | cosΘ | tanΘ | |
| 0度 | 0 | 1 | 0 |
| 30度 | √1/2 | √3/2 | 1/√3 |
| 45度 | √2/2 | √2/2 | 1 |
| 60度 | √3/2 | √1/2 | √3 |
| 90度 | 1 | 0 | ∞ |
| 120度 | √3/2 | -√1/2 | -√3 |
| 135度 | √2/2 | -√2/2 | -1 |
| 150度 | √1/2 | -√3/2 | -1/√3 |
| 180度 | 0 | -1 | 0 |
| 210度 | -√1/2 | -√3/2 | 1/√3 |
| 225度 | -√2/2 | -√2/2 | 1 |
| 240度 | -√3/2 | -√1/2 | √3 |
| 270度 | -1 | 0 | ∞ |
| 300度 | -√3/2 | √1/2 | -√3 |
| 315度 | -√2/2 | √2/2 | -1 |
| 330度 | -√1/2 | √3/2 | -1/√3 |
| 360度 | 0 | 1 | 0 |
具体的には、赤数値のsinΘの0~90度までを、0、√1/2、√2/2、√3/2、1の順番で覚えるだけです。
わざと√(ルート)をつけて覚えてください。√1/2を1/2にしたり、√2/2を2/√2にしないでください。
変換すると、分母と分子のどっちが√やったっけ?と迷子になる可能性が高いからです。
ここが重要ですよ。
直角三角形になる比率(覚えなくてもいい)
試験にでる直角三角形の比率は実は、だいたい決まっています。
そして問題を解いているうちに自然と覚えるので、わざわざ覚えなくてもいいです。
問題を解いているうちに、どうせ同じ比率の問題を提出してるんでしょ?と分かってくるかと思いますよ。
一応以下に比率を記載します。
| ヨコ | タテ | ナナメ |
| 1 | 1 | √2 |
| 1 | √3 | 2 |
| 3 | 4 | 5 |
| 5 | 12 | 13 |
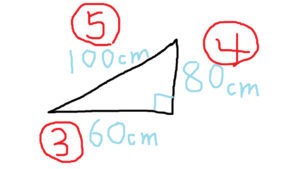
図と表で示したように同じような比率になっていますね。
ヨコ:タテ:ナナメの比率が3:4:5 = 60 : 80 : 100です。
表の完成の仕方

上記を覚えたら、表を埋めていきます。
一度できるようになれば、もう忘れることはないと思いますよ。
ではいきましょうか。
簡単なんで安心してください。
| sinΘ | cosΘ | tanΘ | |
| 0度 | 0 | 1 | 0 |
| 30度 | √1/2 | √3/2 | 1/√3 |
| 45度 | √2/2 | √2/2 | 1 |
| 60度 | √3/2 | √1/2 | √3 |
| 90度 | 1 | 0 | ∞ |
| 120度 | √3/2 | -√1/2 | -√3 |
| 135度 | √2/2 | -√2/2 | -1 |
| 150度 | √1/2 | -√3/2 | -1/√3 |
| 180度 | 0 | -1 | 0 |
| 210度 | -√1/2 | -√3/2 | 1/√3 |
| 225度 | -√2/2 | -√2/2 | 1 |
| 240度 | -√3/2 | -√1/2 | √3 |
| 270度 | -1 | 0 | ∞ |
| 300度 | -√3/2 | √1/2 | -√3 |
| 315度 | -√2/2 | √2/2 | -1 |
| 330度 | -√1/2 | √3/2 | -1/√3 |
| 360度 | 0 | 1 | 0 |
sinΘからいきます。
まず覚えたsinΘ0~90度を表に埋めます。(赤色数値です。)
次に符号は無視して数値のみ、sin90度を基準に180度までひっくり返します。(緑色数値です。)
次に符号は無視して数値のみ、sin180度を基準に360度までひっくり返します。(青色数値です。)
最後に覚えたAll STCを使って、210度~360度の数値にマイナスをつけてsinΘは完成です。
次にcosΘへいきます。
まず覚えたsinΘ0~90度を使用します。(赤色数値です。)
次に符号は無視して数値のみ、sinΘの0~90度の数値を反転してcos0~90度を埋めます。(黄色マーカーです。45度が基準ですね。)
あとはsinΘのときと同様に90~360度まで埋めます。(青色マーカーです。)
次はtanΘへいきます。
覚えた公式sinΘ ÷ cosΘ = tanΘ (これは、S÷C=Tと簡略化)を使って、地道に0~360度の数値を計算して表に埋めます。
最後に覚えたAll STCを使って、90~180度と270~360度の数値にマイナスをつけてtanΘは完成です。(黒色数値です。)
始めは難しく感じるかもしれませんが、5回くらい繰り返せば、脳みそに定着すると思いますよ。長く見積もっても数時間あれば出来るようになるでしょう。
お餅ROI具体的な活用方法

この三角関数の知識ですが、数学の知識として一番役に立っている気がします。
正直理系に進んで数学が何かに役に立っているか?と聞かれると、そこまで役立っていない気がします。
しかし三角関数に関しては、上記の基礎を覚えると応用が利くのです。
使いこなすと周りから頭がいいと思われると思いますよ。
では、解説します。
皆さんは、伊能忠敬(いのうただたか)を知っていますか?
現在まで数々の天才が存在していましたが私が一番天才だと思う偉人が彼です。
この人は1800~1816年かけて日本全国を歩き周り、距離を測量して日本地図を完成させた人です。
現在の日本地図と見比べても約90%以上の正答率だったそうです。
平面の世界にいながら立体的に土地を捉える眼を持ち、まるで日本の上空から眺めているかのごとく地図を完成させてしまう、まさに天才です。
そんな彼が用いた技術がこの三角関数です。
色々な視点から、距離を測量して直角三角形になる地点を参考にして、地図を完成させました。
おそらく自分のノートに三角形がいっぱい記載してあったんでしょうね。そして、後で全ての辻褄が合うようにまとめたと思われます。
この偉人がいたからこそ、日本が鎖国の時に諸外国からの侵略から免れたとさえ言われています。
具体的にはペリー来航です。
ペリーが日本の高精度の地図を見て驚いて逃げ帰ったと言われています。
良ければ、鎖国については以下を参考にしてください。
実生活での活用
この三角関数の技術は我々も使用できます。
もしも、定規やものさしのない世界へいった時に役に立つのです。
例えば無人島でのサバイバル生活やキャンプ場なんかでも活用できるかと思います。
無人島で一つの漂流されたロープの端から端までを1と言う単位に勝手に決めます。
便宜上1ロープとしましょう。
これを問題を解くうちに覚えた比率に当てはめて、(例えば、3対4対5)を活用すれば直角を生かした家が完成します。
具体的には、コンパスの線を引く技術でいけますね。
皆さんはあまり気づいてないですが、我々の生活には直角が至る所に存在しています。
そして皆さんは、直角が好きなのですw逆に言うと直角がないと違和感を感じて気分が悪くなると思いますよ。
上記の通り三角関数を制すれば実生活でも応用できますので、活用してみてください。
例えばDIYとかですね。
良ければ以下も参考にしてください。
教育とは?何の為に学ぶのか?教育の現状と改善策!義務教育の最大の問題点とは?
参考になったら嬉しいです。
ではまた。



コメント